Packing hex numbers in JavaScript, part 2

This is a follow-up to my previous article about the Golf Horse “SIGBOVIK” problem. With great effort, I managed to save 6 bytes from the last submission, auroch_v4, described there. In this article, I’ll give an in-depth explanation of the additional techniques I used and how I discovered them. If you just want to see the code, a sanitized version of my source is on GitHub.

TL;DR

The remainder of this article is excessively detailed because I think it’s interesting, but that may distract from the main points. So, here’s a quick explanation of the bytes saved:

for(...;c=DATA.charCodeAt(i/2);...)e=e*9.1^c →
for(...;e+=e/DATA.charCodeAt(i/2);...)
Saved 3 bytes by switching to an extremely simple “hash” function: saved 6 bytes of code, but lost 3 bytes of compressed data. One byte of the losses is explainable by reduced degrees of freedom in the hash’s parameters. The other 2 bytes I don’t have a theoretical explanation, but I suspect the hash function just isn’t as good, causing some loss of entropy.

(e&15).toString(16) →
e.toString(16)[12]
Saved 1 more byte of code by changing how we get hex digits. Note that this optimization is dependent on the hash function—it wouldn’t have been possible with auroch_v4’s hash, for example (for reasons explained later). Why 12 and not a single digit index, like 9, to save another byte? Anything less than 10 didn’t work because it would sometimes pick up the decimal point instead of a hex digit.

for(w=e=i=``;...;w+=++i%65?e.toString(16)[12]:` `);console.log(w) →
for(w=e=i=1;...;)w=++i%65?e.toString(16)[12]+w:[console.log(w)]
Saved 1 byte with how we produce newlines in the output, taking advantage of JavaScript’s quirky behavior when Array is coerced to String. Two bytes of code saved, one byte lost in the compressed data string for padding.

Saved 1 byte of compressed data by including 4-byte UTF-8 characters and invalid (!) UTF-8 in the encoder’s search.

Total: 6 bytes saved.

Areas for improvement

As discussed in the previous article, the general template for my submissions looks like this:

w="" //stores the output
e=1  //number from which we will extract our hex digits (e stands for "entropy")
for(i=1;i<845;)
{
  //hash() is a hashing function, DATA is the compressed data
  e=hash(e,DATA.charCodeAt(i/2))

  //Add a hex digit or a newline to our output
  w+=i++%65?(e&15).toString(16):`\n`
}

//Write the output
console.log(w)

The general idea is to build the hex numbers one digit at a time, by extracting a single hex digit from a number which is continually hashed with the compressed data. With a good enough hash function (and a good enough encoder!), it produces hex digits from a string at nearly the entropy limit imposed by UTF-8 JavaScript.

auroch_v4 looked like this (with small readability changes):

for(w=e=i=``;c=DATA.charCodeAt(i/2);w+=++i%65?(e&15).toString(16):`\n`)
  e=e*9.1^c
console.log(w)

The code size is already very small, but there are several areas that are worth revisiting:

1. Is the intermediate variable c really necessary? We could save a byte or two if there’s a way to combine c=DATA.charCodeAt(i/2) and e=e*9.1^c into a single expression. But it’s not obvious how to do that without breaking the loop termination condition.
2. Is (e&15).toString(16) the shortest way to get a single hex digit out of e? Is there a way to make something like e.toString(16)[0] work?
3. Is our method for inserting newlines w+=++i%65?...:`\n` the best possible?
4. We index into the compressed data by using i/2. Is that optimal? For example, what about i*.49 or i*.51?

There are also questions about the encoding process:

5. The encoder didn’t consider 4-byte UTF-8 characters, due to the issues it raises with JavaScript’s UTF-16 strings. Can we utilize 4-byte characters?
6. I couldn’t perform a complete search for the optimal compressed data. Could we estimate how much improvement could come from a complete search?

I’d group together 1–3 as “golf tricks”, and 4–6 as algorithmic questions. We’ll do a deep dive into each of these areas—some will turn out to be fruitful, some not!

Golf tricks

The starting point for many of the code optimizations was #1: when I realized there’s a way to combine the hashing code c=DATA.charCodeAt(i/2) and e=e*9.1^c. auroch_v4 used this code:

for(...;c=DATA.charCodeAt(i/2);...)e=e*9.1^c

The loop termination is a critical trick in this code: when i gets large enough, we read past the end of DATA. That produces an undefined value, which is falsy and terminates the loop. If we were instead to do

for(...;e=e*9.1^DATA.charCodeAt(i/2);...)  //doesn't work

This doesn’t work because the XOR operator casts undefined to 0, and so e remains truthy, and our loop won’t terminate.

There are two changes needed to make this work: first, replacing XOR with addition, so that undefined doesn’t get coerced to 0 anymore:

for(...;e=e*9.1+DATA.charCodeAt(i/2);...)  //better, but still doesn't work

This will now terminate the loop at the correct time, but we introduced a problem: e will eventually overflow because it’s no longer getting truncated (the XOR operator truncates to 32 bits). We can fix that by using the NOT operator to truncate e at each iteration:

for(...;e=~e*9.1+DATA.charCodeAt(i/2);...)  //this works! auroch_v5

This saves 2 bytes compared to auroch_v4, and it’s what I submitted as auroch_v5 (after re-running the encoder for the new hash function). However, that wasn’t the end of the optimizations.

Abandoning bitwise operators

All the hash functions I had tried up to this point involved a bitwise operation. These operations truncate to 32 bits, but a Number (being a 64-bit double) has almost 64 bits of state, so we’re losing a lot of potential state space. I had reason to believe (explained in a later section) that additional state space could potentially save a byte in the encoding, so I wanted to see if there were any good options for hashing without a bitwise operator. It took me many attempts to find some hashes that worked and had small code size, and one early success was this:

for(...;e=e**.1*DATA.charCodeAt(i/2);...)  //"Exponential hash"

Whereas auroch_v5 and its predecessors all relied on bit operations to keep e bounded, now we use the exponential operator **.1 to keep e from overflowing. This saves a byte of code compared to auroch_v5. However, it has the disadvantage that we can no longer use the Unicode character 0 in the compressed data, as that will cause e to get stuck at 0. It also had the disadvantage that the parameter space was much smaller: in auroch_v5, we could test many multipliers (and also divisors, such as e/.13) to find one that gets lucky, whereas this new hash function only has a single-digit exponent to search over. Altogether, this didn’t save any bytes—but it unlocked a new optimization that did!

Hex digit extraction

As mentioned in area for improvement #2, we’ve been getting hex digits from e by doing (e&15).toString(16). I had always wanted to try e.toString(16)[X] instead to save a couple bytes, but this wouldn’t work in auroch_v5 or its predecessors. The reason is that if X is too small (say, 4 or less), then we’re reading from bits of e that don’t have a lot of entropy—most of the bit-mixing in e happens in the rightmost bits. If X is too large (say, 5 or more), then we fail right away because e starts small and doesn’t have 5 digits!

The “exponential hash” above doesn’t have the latter problem: e always has lots of digits, so now a moderate value of X works (with some caveats about avoiding the decimal point). As an illustrative example,

for(w=e=i=2;e=e**.1*`-% $...`.charCodeAt(i/2);)w+=i++%65?e.toString(16)[7]:'\n';console.log(w)

i     DATA.charCodeAt(i/2)    e.toString(16)
--------------------------------------------
                              2
2     37                      27.a7d696b59ec8
3     37                      35.75dcb6d22de
4     2                       2.fa351a70307f
5     2                       2.3b05c7da2ee64
6     32                      22.ac4927a0252c
7     32                      2d.9e8dd57b1e06

The highlighted digits correspond to e.toString(16)[7], and we can see they form the beginning of the correct output: 29ba72dc7….

I should mention that this new way of getting hex digits was a huge burden on the encoder: e.toString(16)[X] is an incredibly slow operation compared to e&15, and my encoder needed to do this many billions of times! I wrote my own routine to calculate e.toString(16)[X] using only numeric operations to help performance, but even then, I lost a factor of about 10x speed. The encoder’s runtime went from hours to days!

A Hail-Mary hash function

Our exponential hash is very short, but I wanted to make sure I was finding every last byte of savings! As a last-ditch attempt, I started enumerating the shortest possible expressions that had any chance of working, and one candidate actually did:

for(...;e+=e/DATA.charCodeAt(i/2);...)  //auroch_v6

In some ways, this is a terrible hash function. The lower bits of e are almost irrelevant, and the upper bits only mix slowly. Furthermore, at first, it did not even appear to work, because e keeps growing and the decimal point keeps moving. e.toString(16)[X] did not work for any single-digit X; only 10–13 would avoid the decimal point without reading past the end.

That said, the code size savings were significant: 3 bytes compared to the exponential hash. A couple bytes were lost in the compressed data, probably because of the poor quality of the hashing, but that’s still a byte saved overall.

Newline optimization

Finally, the last golf trick is for #3: inserting newlines into the output. auroch_v5 and its predecessors all used this approach:

for(...)w+=i++%65?get_hex_digit(e):`\n`;console.log(w)

Having honed my skills at code.golf the last few months, I was able to discover a small savings:

for(...)w=++i%65?w+get_hex_digit(e):[console.log(w)]

Instead of building one large string w and then printing it, now we print one line at a time. The trick here is that console.log always returns undefined, and [undefined] coerces to an empty string (one of many questionable JavaScript behaviors!), thus giving us an efficient way to re-initialize w after printing.

This saves two bytes of code, but requires an extra byte in the compressed data for padding, because we need to run one more iteration of the loop to print the last line. Net savings of 1 byte.

Going backward

Another benefit of this newline optimization is that we can also generate the data backward:

w=++i%65?w+get_hex_digit(e):[console.log(w)]  //forward
w=++i%65?get_hex_digit(e)+w:[console.log(w)]  //backward

Backward turned out to be a better approach, because it wasted less entropy from the compressed data. The reason is a bit hard to explain, but it has to do with the interaction of how we initialize our variables, how the compressed data is read, and the padding required to ensure we loop for the correct number of iterations:

for(w=e=i=1;DATA.charCodeAt(i/2);i++)  //Option 1
for(w=e=i=2;DATA.charCodeAt(i/2);i++)  //Option 2

Recall that w holds the output. So, the initial value of w must match the beginning of the output. Because no SIGBOVIK numbers begin with a 1, and none end with a 2, Option 1 requires the backward approach and Option 2 requires the forward approach.

Option 1 will only generate one hex from the first character of DATA (when i is 1). The last character of DATA is used only for padding, and its value is irrelevant.

Option 2 never reads the first character of DATA (since i starts at 2), and it only generates one hex from the last character of DATA.

These two choices sound similar, but there’s a subtle reason why Option 1 is better. Each character theoretically has about 8.14 bits of entropy (as calculated in the previous article; although with the Unicode tricks described below, it goes up to 8.19 bits), so it can be wasteful to generate only one 4-bit hex from a character. Though Option 1 only gets one hex from the first character, e is forever affected by its value—it continues to carry the extra entropy of the first character. Whereas in Option 2, when the last character generates the last hex, the extra entropy of the last character never has a chance to be used. So, Option 2 effectively loses a few bits of entropy from the last character.

To be thorough, I’ll point out that Option 2 has a small advantage: there are two SIGBOVIK numbers beginning with 2, while only one SIGBOVIK number ends with 1. That extra degree of freedom gives Option 2 a one-bit theoretical savings, but that’s not enough to offset Option 1’s advantage.

Unicode tricks

As mentioned in area for improvement #5, I was too quick to dismiss 4-byte UTF-8 characters in my previous attempts.

First, some background on Unicode and JavaScript. The golf horse website accepts programs in the UTF-8 format, but JavaScript itself doesn’t use UTF-8 for strings. JavaScript, like many systems and programming languages of the time, decided to use 16-bit characters as the basis for its string datatype, as that was adequate to hold any Unicode code point prior to 2001. However, Unicode grew past 16 bits, and so there’s some awkward behavior when dealing with characters outside the 16-bit range.

1–3 byte UTF-8 characters all fit in 16 bits. However, when a 4-byte UTF-8 character is decoded in JavaScript, it becomes a 2-character string—a surrogate pair as per UTF-16. When using charCodeAt, this single Unicode character appears as two JavaScript characters:

s = "\u{2F804}"      //one Unicode character which would be 4 bytes in UTF-8
s.length === 2       //appears as 2 JavaScript characters
s.charCodeAt(0) === 0xD87E
s.charCodeAt(1) === 0xDC04

Often this is undesirable behavior, and that’s why JavaScript also provides codePointAt and a Unicode-aware iterator for String. However, for our purposes, we don’t need Unicode correctness, we just need numbers we can hash. If we put a 4-byte UTF-8 character into a string, it’ll simply come out as two JavaScript characters we can access with charCodeAt.

It’s uncommon that a 4-byte character actually comes in useful; my calculations suggest that in an optimal encoding, only about 1 in 400 characters would be 4 bytes, and only 0.2 bytes would be saved in expectation. Nevertheless, I upgraded my encoder to also search through 4-byte characters.

WTF-8

JavaScript strings aren’t restricted to valid UTF-16; they can hold unmatched surrogates (i.e., the code points U+D800 to U+DFFF). Though this is disallowed by the Unicode standard, there’s an obvious way to encode these in UTF-8 (sometimes known as WTF-8). So, I was wondering what would happen if I tried these disallowed characters in my source code. What happened is that v8 (the JavaScript engine used by golf horse, not to mention Chrome and Node.js) replaced all the illegal bytes with U+FFFD, which I learned is the “replacement character” to represent errors.

That meant I couldn’t create unpaired surrogates in my JavaScript strings. However, it gave me an easy way to put U+FFFD into my strings: I just had to put an illegal byte into my source code! Specifically, if I put the byte 0xFF into the source code (which is never a legal byte in UTF-8), v8 would replace it with U+FFFD upon loading the program.

Basically, we gained access to a new 1-byte character we can put in our strings. We used to have 125 options for 1-byte characters (all the 1-byte UTF-8 characters except backtick, carriage return, and backslash), now we have 126. Having this additional character saves about 0.5 bytes in expectation.

This felt a bit like cheating—I’m now submitting programs that aren’t even valid UTF-8. But it’s in the spirit of code golf to exploit any advantage possible!

Together, 4-byte characters and illegal UTF-8 save 0.7 bytes in expectation, which materialized into a full byte saved.

	auroch_v4	auroch_v5	auroch_v6
1–3 byte UTF-8	✅	✅	✅
4 byte UTF-8	❌	✅	✅
Invalid UTF-8	❌	✅	✅
Cache size	\(5 \cdot 10^6\)	\(16 \cdot 10^6\)	\(16 \cdot 10^6\)
Run time	~ 4 hours x ~4 runs	~ 5 hours * x ~10 runs	~ 48 hours x 4 runs
Best solution (length of compressed data excluding padding)	464 bytes	463 bytes	466 bytes **

* auroch_v5’s encoder contained performance enhancements, so despite the larger search space, it ran about the same time as auroch_v4’s
** Lost 3 bytes due to auroch_v6’s different hash function. As mentioned earlier, its new hash had fewer degrees of freedom, costing 1 byte; and 2 bytes lost apparently due to its worse bit-mixing properties.

Optimal indexing

In this section, I’d like to show one idea that didn’t work out, but I thought was interesting to explore.

As mentioned in area for improvement #4, we are accessing the compressed data using DATA.charCodeAt(i/2). The question is whether i/2 is the best possible formula for indexing into the data.

As mentioned earlier, each character of DATA is theoretically worth about 8.19 bits. We have a total of 832 hexes (13 numbers, 64 hexes in each number), so the ideal length of DATA is \(832 \cdot 4/8.19 \approx 407\) characters. However, i must go up to 845 (to get 832 hexes plus 13 newlines). That suggests the optimal indexing into DATA should be i*407/845 rather than i/2. Of course, we need to consider the tradeoff of using a longer formula versus how many bytes of DATA we expect to save.

To answer this question, we can build a model of how much entropy we have in strings with C characters and B bytes. Let f(B,C) be the number of strings with C characters and B bytes. Then f satisfies the recurrence

f(B,C) = (# 1 byte characters) * f(B-1, C-1)
       + (# 2 byte characters) * f(B-2, C-1)
       + (# 3 byte characters) * f(B-3, C-1)
       + (# 4 byte characters) * f(B-4, C-1)

We need \(832 \cdot 4\) bits of entropy to represent all the SIGBOVIK numbers (actually a bit less due to degrees of freedom; we’ll quantify this later), so we need f to be approximately \(L=2^{832 \cdot 4}\). So, let’s crunch some numbers:

Indexing Formula	# Characters	f(Bytes, Characters)
i/2	845 / 2 = 423	f(466, 423) = L * 0.06 f(467, 423) = L * 11.0
i/2.1	845 / 2.1 = 403	f(466, 403) = L * 0.44 f(467, 403) = L * 56.7
i*.48	845 * .48 = 406	f(466, 406) = L * 0.53 f(467, 406) = L * 72.6
i*.49	845 * .49 = 415	f(466, 415) = L * 0.35 f(467, 415) = L * 55.9

These calculations suggest that we’re going to have 466–467 bytes of compressed data regardless of which formula we choose. Since changing the formula adds two bytes and saves at most one, this isn’t a profitable change.

It’s worth noting that if we include the degrees of freedom—the ability to reorder the output and to change the hash function’s parameters—the entropy needed is reduced by around 31–39 bits (depending which hash function is used; 39 for auroch_v5 and 31 for auroch_v6). Redoing the calculations, that suggests the theoretically smallest compressed data would be around 5 bytes less than suggested here. Using the i/2 indexing formula, that suggests 461 or 462 would be the theoretically optimal size for the compressed data. That’s a bit optimistic, since it’s assuming a perfect hash (i.e., every string of compressed data would give a different program output). Yet auroch_v5 got close, achieving 463 bytes of compressed data.

Convergence testing

Finally, let’s look at area for improvement #6: how much savings could we expect from a perfect encoder? The above calculation suggests we have at most 2 bytes to save. Is that just theoretical, or could a better encoder achieve that?

As described in my previous article, my encoder can be summarized as a beam search, or dynamic programming with a limited cache of states. It is very heavy with both CPU and memory: auroch_v6 used 10GB of memory and ~48 hours of CPU time per encoding. Indeed, the cache size of 16 million was running up against v8’s limit of \(2^{24}\) elements in a Set (though to be fair, it’s not hard to work around this limitation).

That said, I figured it was still possible to do bigger searches. Multithreading could give access to more CPU power, and a specialized data structure could store the cache more efficiently (although I was extremely impressed how well v8 packed the JavaScript objects). This would be a lot of effort, so I wanted to determine whether it would be worth pursuing.

First, I did some empirical testing with auroch_v5’s encoder. I tried several different multipliers in the hash function and varied the cache size.

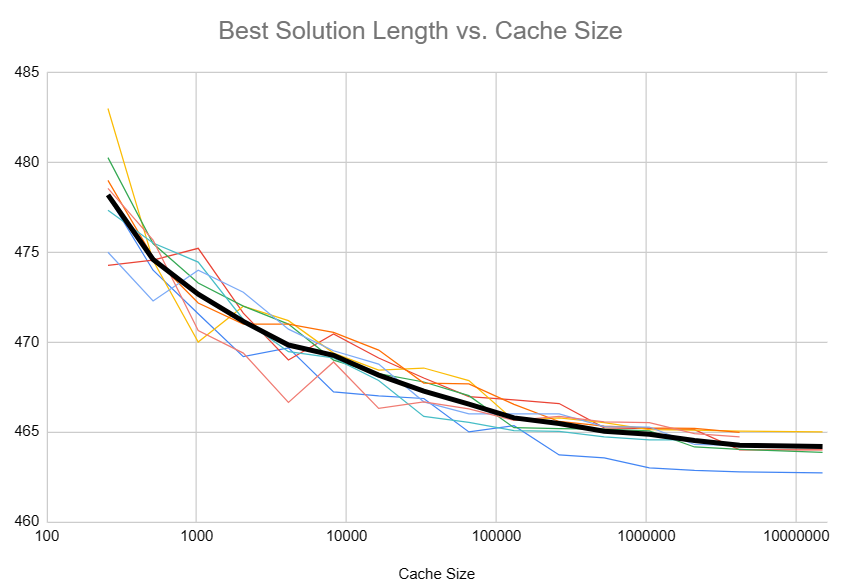
Plotting the results, the diminishing returns are apparent, and I gained confidence that a cache size of \(16 \cdot 10^6\) was adequate.

I also attempted to build a theoretical model of how the encoder worked. This was my idea for the model:

• Track the number of solutions in the cache of each length (measured in bytes).
• For each element of the cache, append all possible characters and put the results in a new cache. Again, we only track the length of the solutions in the new cache.
• Assume only 1/256 solutions will work, since we need two hexes from each character and (assuming a perfect hash) it’s random whether the hexes are correct.
• After each step, trim the cache down to the best X elements, where X is a parameter we can vary.

The model is limited, so I can’t trust it too much. It doesn’t consider the newlines happening every 65 iterations or the ability to reorder the output, and it assumes a perfect hash function. However, the model worked well in the sense that with a large enough cache size, its results agreed with my theoretical calculations.

The results I got were interesting:

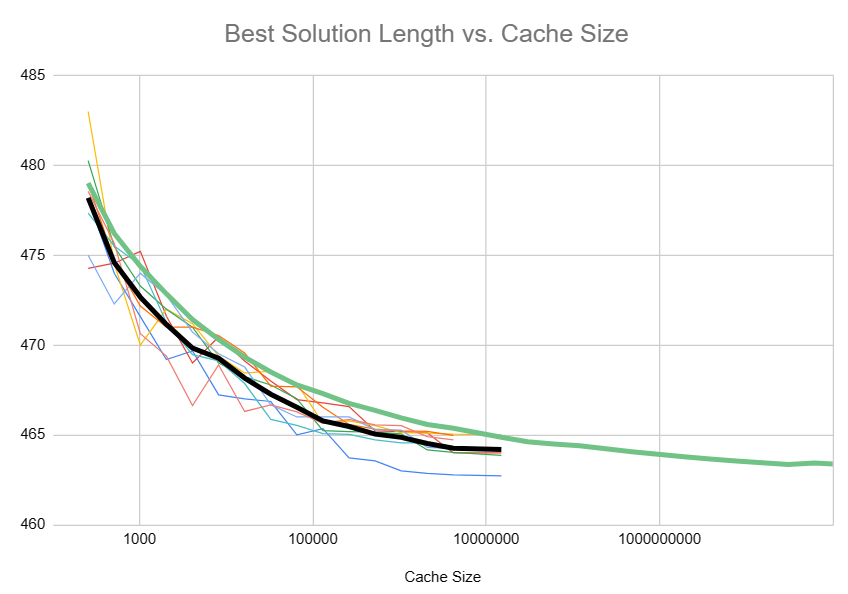
The model was under-predicting the empirical rate of convergence, and it suggested there’s another two bytes to be saved if we can increase the cache size to \(10^{11}\). The prediction of two bytes saved is especially interesting, because my theoretical calculations (from the previous section) suggest that with a perfect hash, the best possible solution length is 461, compared to auroch_v5’s result of 463—a two byte difference.

I suspect that the critical factor here is that the model is assuming a perfect hash, which we don’t have. In auroch_v5, the hash is on a 32-bit integer, so we have a limited state space—we could never utilize a cache size of \(10^{11}\) because we only have about \(4\cdot 10^9\) states! Limiting the model to \(2^{32}\) states, it shows a loss of 1.25 bytes. In fact, 4 bits of the hash are implied by the last hex we had to get, so the state space is really just \(2^{28}\), which the model shows as losing 1.8 bytes. Altogether, that seems consistent with 463 bytes being the true optimum. (The fact that 32 bits of state is so limiting is what originally motivated me to look for hashes that utilized more of the potential 64 bits in a Number.)

I didn’t do similar tests on auroch_v6 because it’s simply too slow. However, that won’t stop me from speculating! While auroch_v6 had ~50 bits of state from using a double-precision number (64 bits for a double, minus several bits at the end of the mantissa that never get used, minus several bits of exponent that never get used, minus the sign bit that never gets used), the hash function simply isn’t very good, so I don’t think most of that state is relevant. I’d actually expect less than 32 bits of effective state space, and therefore easier to search for optimal solutions than auroch_v5. So, my bold guess is that auroch_v6’s encoder should’ve been able to find an optimal solution.

Final thoughts

If you made it this far, I hope you enjoyed all the minutiae of this golf problem as much as I did.

I feel like I’ve exhausted this problem, finding every byte that I could. There’s always a possibility for more tricks I’ve missed, but I don’t even know where to look for one!

I hope I’ll be able to apply the bit-packing techniques here to other golf problems; the same techniques should generalize for packing other types of data.