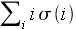 , where
, where 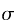 is a random permutation on the numbers 1 through N, and i ranges from 1 through N. See also A056876.
is a random permutation on the numbers 1 through N, and i ranges from 1 through N. See also A056876.
Linear regressions have a fairly strict set of assumptions that need to be satisfied to make meaningful conclusions about the p-value or estimation error, such as normality and independence of the residuals. Moreover, many data sets do not satisfy these assumptions, even though many statistics books would have one believe most things are distributed normally. For example, most financial data sets are fat-tailed.
At the expense of producing a predictive model, Spearman Rho is a much more robust test for the existence of a monotonic relationship between the variables. However, the null distribution is more complex, so it's also more difficult to obtain an accurate p-value. (I'd argue an exact p-value is far less important than knowing certainly that the model assumptions hold!) The computation below shows the exact null distribution for small sample sizes.
Furthermore, the null distribution is also related to a number theory problem of intrinsic interest: the distribution of 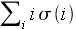 , where
, where 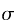 is a random permutation on the numbers 1 through N, and i ranges from 1 through N. See also A056876.
is a random permutation on the numbers 1 through N, and i ranges from 1 through N. See also A056876.
Unfortunately, until now, there was little data freely available on the internet about this distribution. Several statistics papers have discussed it, but the only free one I can find is here (Fast computation of the exact null distributio of Spearman's rho and Page's L statistic for samples with and without ties, M.A. van de Wiel and A. Di Bucchianico).
Note: I've discovered an algorithm with better complexity but haven't implemented it yet. See the next section for details.
As in the aforementioned paper, a convenient technique for calculating the distribution of 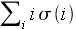 , from which one easily obtains the Spearman Rho null distribution, is using the permanent of
, from which one easily obtains the Spearman Rho null distribution, is using the permanent of 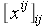 . One can verify that the coefficient of xi is the frequency for the sum i. So, this computation is equivalent to calculating the permanent of a certain symmetric matrix of monomials.
. One can verify that the coefficient of xi is the frequency for the sum i. So, this computation is equivalent to calculating the permanent of a certain symmetric matrix of monomials.
The paper uses a Laplace-type expansion for the permanent, and then by factoring out powers of x and using symmetry, a great deal of computation can be reused. They do not provide a complexity analysis or timing results, but it appears to be O(2nn5) on a cursory look. (We assume arithmetic operations have constant cost. In reality, precision of n log n is required.) It also appears to require a fair amount of memory for the reusable computations, although they do not address this in the paper.
Instead, I opted to use Ryser's formula,
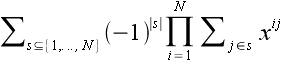
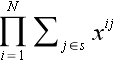 for a subset s+1 is just xn(n+1)/2 times the product for s. This halves the number of terms needed in Ryser's formula, although its impact is smaller on computation time.
for a subset s+1 is just xn(n+1)/2 times the product for s. This halves the number of terms needed in Ryser's formula, although its impact is smaller on computation time.My program is a fairly straightforward implementation of the above in C++, no fancy assembly or other low-level coding was used. 96-bit integers were used, which should accommodate N through 30. (Note that intermediate results exceed the 96-bit limit. However, this just means the computation is done modulo 296, and the final result is still valid.) The platform is Win32, compiled with gcc. I may make the source available after cleaning it up, but I would also like to try some other optimizations, such as CPU vector operations.
An algorithm with better complexity
I did also find an algorithm with better complexity. Simply choose O(n3) values for x and compute the permanent. The generating function for the distribution can be recovered using polynomial interpolation techniques. Using an efficient implementation of Ryser's formula, the permanent takes time O(2nn), thus we arrive at complexity O(2nn4). Again, this is the number of arithmetic operations; n log n bits of precision are required.
Below are tables of the exact distribution.
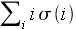
Note that the results of a computation are NOT copyrighted. Therefore you may freely use these tables. Of course, a citation would be appreciated.
n = 3
n = 4
n = 5
n = 6
n = 7
n = 8
n = 9
n = 10
n = 11
n = 12
n = 13
n = 14
n = 15
n = 16
n = 17
n = 18
n = 19
n = 20
n = 21
n = 22
n = 23
n = 24
n = 25
n = 26
The timings are on a 2GHz Core 2 Duo, Win32. All numbers are in seconds. This doesn't particularly follow O(2nn5), apparently due to cache and memory effects.
| n | 64 bits | 96 bits | ||
|---|---|---|---|---|
| 3 | 0.000003 | 0.000005 | ||
| 4 | 0.000015 | 0.000009 | ||
| 5 | 0.000014 | 0.000027 | ||
| 6 | 0.000055 | 0.000096 | ||
| 7 | 0.000172 | 0.000370 | ||
| 8 | 0.000636 | 0.001466 | ||
| 9 | 0.002237 | 0.003279 | ||
| 10 | 0.007955 | 0.01210 | ||
| 11 | 0.02566 | 0.03730 | ||
| 12 | 0.08103 | 0.1204 | ||
| 13 | 0.2500 | 0.3600 | ||
| 14 | 0.7608 | 1.079 | ||
| 15 | 2.090 | 3.195 | ||
| 16 | 5.848 | 9.528 | ||
| 17 | 16.09 | 28.07 | ||
| 18 | 43.68 | 83.09 | ||
| 19 | 116.9 | 234.8 | ||
| 20 | 300.5 | 940.1 | ||
| 21 | 1963 | |||
| 22 | 4851 | |||
| 23 | 17600 | |||
| 24 | 41240 | |||
| 25 | 124800 | |||
| 26 | 316200 |